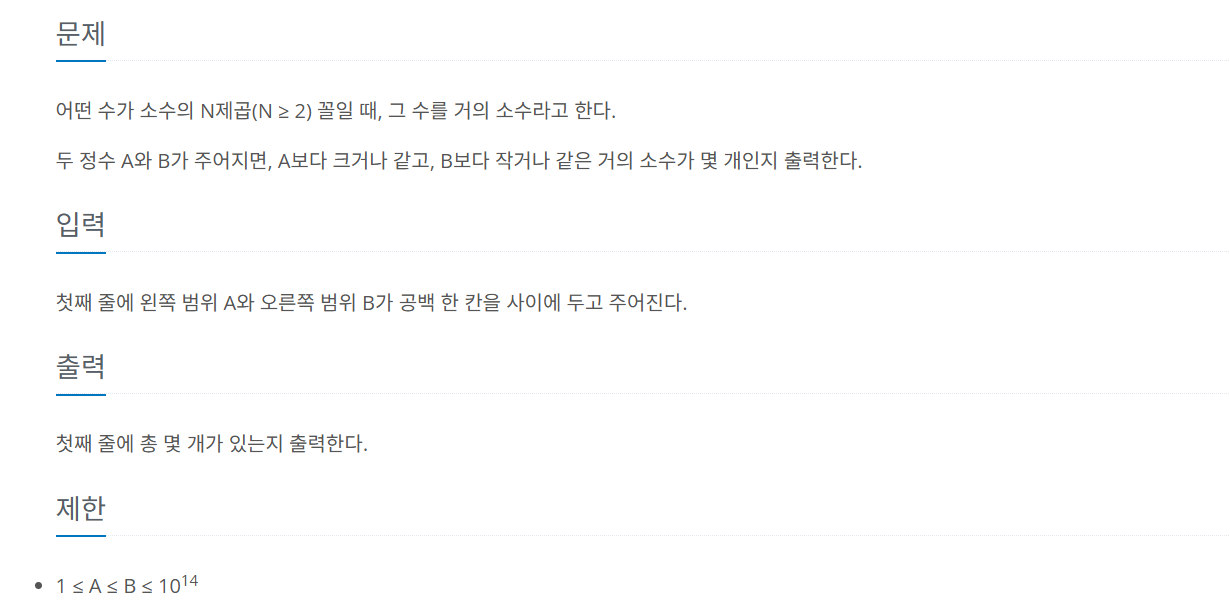
#1456 - 거의 소수
난이도: 골드5
문제 유형: 정수론, 소수
https://www.acmicpc.net/problem/1456
문제 분석
최대 범위에 해당하는 모든 소수를 구한 뒤, 이 소수들이 입력된 A와 B 사이에 존재하는지 판단하여 문제를 해결할 수 있다.
입력에서 주어진 최댓갑신 10^14까지 소수를 탐색하는 것이 아니라 에라토스테네스의 체를 이용하여 소수를 구할 것이기 때문에 10^14의 제곱근인 10^7까지의 소수를 탐색해줄 것이다.
후에는 주어진 소수들이 A~B 범위 안에 속하는지 판별하여 유효한 소수개수를 결과로 출력해주면 된다.
1. 2 ~ 10,000,000 사이에 존재하는 모든 소수를 구한다.
2. 각각의 소수에 관해 소수를 N제곱한 값이 B보다 커질 때까지 반복문을 실행한다. 이때 소수를 N제곱한 값이 A보다 크거나 같으면 거의 소수로 판단하여 카운트해준다. 이를 이용해 A~B 범위의 거의 소수들의 갯수를 구할 수 있다.
- 이렇게 구현할 시 N제곱한 값을 구하는 도중 값의 범위가 long형을 초과하는 경우가 발생한다.
예를 들어
소수 p = 2인 경우
2¹ = 2
2² = 4
2³ = 8
2⁴ = 16
...
2⁶¹ ≈ 2.3 * 10¹⁸ (아직 long 범위 내)
2⁶² ≈ 4.6 * 10¹⁸ (아직 long 범위 내)
2⁶³ ≈ 9.2 * 10¹⁸ (long 범위 거의 도달)
2⁶⁴ ≈ 18.4 * 10¹⁸ (long 범위 초과!)
위와 같은 경우에 long 범위를 초과할 수있다. 따라서 계산의 오류를 방지하기 위해 N^k와 B값이 아닌 이항정리를 활용하여 N과 B/(N^(k-1)) 을 비교하는 형식을 써야한다.
여기서 이항정리를 활용하여 비교한다는게 무슨 말인지 정리해보겠다.
원래 하려던 비교
N^k ≤ B
이항정리를 활용한 비교
N ≤ B/(N^(k-1))
예시
N = 2, B = 100인 경우 k=5일 때를 확인하고 싶다면
기존 방식: 2⁵ ≤ 100 를 확인하려면 32 ≤ 100 을 직접 계산
이항정리 활용: 2 ≤ 100/(2⁴) 2 ≤ 100/16 2 ≤ 6.25 를 계산
이렇게 변환하는 이유는
- N^k를 직접 계산하면 k가 커질수록 값이 매우 커져서 long 범위를 초과할 수 있음
- 하지만 B/(N^(k-1))로 변환하면 분모와 분자가 서로 상쇄되어 더 작은 수로 계산 가능
- 수학적으로는 동일한 비교지만, 실제 계산에서는 overflow를 방지할 수 있음
위와 같은 이유로 A~B 범위 내에 거의 소수를 판별하기 위한 식으로 이항정리를 활용하기로 하였다.
전체 코드를 보자
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] st = br.readLine().split(" ");
long m = Long.parseLong(st[0]);
long n = Long.parseLong(st[1]);
long[] arr = new long[10000001];
int cnt = 0;
for(int i = 2; i< arr.length; i++){
arr[i] = i;
}
for(int i = 2; i<= Math.sqrt(arr.length); i++){
if(arr[i] == 0){
continue;
}
for(int j = i + i ; j< arr.length; j= j + i){
arr[j] = 0;
}
}
for(int i = 2; i<= 10000000; i++){
if(arr[i] != 0){
long tmp = arr[i];
while((double)arr[i] <= ((double)n/(double)tmp)){
if((double)arr[i] >= ((double)m/(double)tmp)){
cnt++;
}
tmp = tmp * arr[i];
}
}
}
System.out.println(cnt);
}
}
위 코드에서 유심하게 볼 부분은
long tmp = arr[i];
while((double)arr[i] <= ((double)n/(double)tmp)){
if((double)arr[i] >= ((double)m/(double)tmp)){
cnt++;
}
tmp = tmp * arr[i];
}
이 부분이다.
1. (double)arr[i] <= ((double)n/(double)tmp)
- 이는 다음 거듭제곱이 n을 넘지 않는지 확인
- tmp * arr[i] ≤ n 을 검사하는 것과 동일
- overflow를 방지하기 위해 나눗셈 형태로 변환
2. (double)arr[i] >= ((double)m/(double)tmp)
- 현재 거듭제곱이 m보다 크거나 같은지 확인
- tmp * arr[i] ≥ m 을 검사하는 것과 동일
- 마찬가지로 overflow 방지를 위해 나눗셈 사용
수학적인 개념이 적용되는 문제들은 아직 잘 모르겠다. 수학이 많이 약해서 생기는 현상이라 생각한다. 수학쪽을 좀 더 공부할 필요가 있을 것 같다.
'PS' 카테고리의 다른 글
| [Java] 백준 22858번 - 원상 복구 (small) (0) | 2024.09.12 |
|---|---|
| [Java] 백준 13023번 - ABCDE (2) | 2024.07.20 |
| 프로그래머스 - 주식가격 (스택/큐) (0) | 2023.05.10 |
| 프로그래머스 - 프로세스 (스택/큐) (0) | 2023.05.09 |
| 프로그래머스 - 다리를 지나는 트럭 (스택,큐) (0) | 2023.05.06 |
#1456 - 거의 소수
난이도: 골드5
문제 유형: 정수론, 소수
https://www.acmicpc.net/problem/1456
문제 분석

최대 범위에 해당하는 모든 소수를 구한 뒤, 이 소수들이 입력된 A와 B 사이에 존재하는지 판단하여 문제를 해결할 수 있다.
입력에서 주어진 최댓갑신 10^14까지 소수를 탐색하는 것이 아니라 에라토스테네스의 체를 이용하여 소수를 구할 것이기 때문에 10^14의 제곱근인 10^7까지의 소수를 탐색해줄 것이다.
후에는 주어진 소수들이 A~B 범위 안에 속하는지 판별하여 유효한 소수개수를 결과로 출력해주면 된다.
1. 2 ~ 10,000,000 사이에 존재하는 모든 소수를 구한다.
2. 각각의 소수에 관해 소수를 N제곱한 값이 B보다 커질 때까지 반복문을 실행한다. 이때 소수를 N제곱한 값이 A보다 크거나 같으면 거의 소수로 판단하여 카운트해준다. 이를 이용해 A~B 범위의 거의 소수들의 갯수를 구할 수 있다.
- 이렇게 구현할 시 N제곱한 값을 구하는 도중 값의 범위가 long형을 초과하는 경우가 발생한다.
예를 들어
소수 p = 2인 경우
2¹ = 2
2² = 4
2³ = 8
2⁴ = 16
...
2⁶¹ ≈ 2.3 * 10¹⁸ (아직 long 범위 내)
2⁶² ≈ 4.6 * 10¹⁸ (아직 long 범위 내)
2⁶³ ≈ 9.2 * 10¹⁸ (long 범위 거의 도달)
2⁶⁴ ≈ 18.4 * 10¹⁸ (long 범위 초과!)
위와 같은 경우에 long 범위를 초과할 수있다. 따라서 계산의 오류를 방지하기 위해 N^k와 B값이 아닌 이항정리를 활용하여 N과 B/(N^(k-1)) 을 비교하는 형식을 써야한다.
여기서 이항정리를 활용하여 비교한다는게 무슨 말인지 정리해보겠다.
원래 하려던 비교
N^k ≤ B
이항정리를 활용한 비교
N ≤ B/(N^(k-1))
예시
N = 2, B = 100인 경우 k=5일 때를 확인하고 싶다면
기존 방식: 2⁵ ≤ 100 를 확인하려면 32 ≤ 100 을 직접 계산
이항정리 활용: 2 ≤ 100/(2⁴) 2 ≤ 100/16 2 ≤ 6.25 를 계산
이렇게 변환하는 이유는
- N^k를 직접 계산하면 k가 커질수록 값이 매우 커져서 long 범위를 초과할 수 있음
- 하지만 B/(N^(k-1))로 변환하면 분모와 분자가 서로 상쇄되어 더 작은 수로 계산 가능
- 수학적으로는 동일한 비교지만, 실제 계산에서는 overflow를 방지할 수 있음
위와 같은 이유로 A~B 범위 내에 거의 소수를 판별하기 위한 식으로 이항정리를 활용하기로 하였다.
전체 코드를 보자
public class Main { public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); String[] st = br.readLine().split(" "); long m = Long.parseLong(st[0]); long n = Long.parseLong(st[1]); long[] arr = new long[10000001]; int cnt = 0; for(int i = 2; i< arr.length; i++){ arr[i] = i; } for(int i = 2; i<= Math.sqrt(arr.length); i++){ if(arr[i] == 0){ continue; } for(int j = i + i ; j< arr.length; j= j + i){ arr[j] = 0; } } for(int i = 2; i<= 10000000; i++){ if(arr[i] != 0){ long tmp = arr[i]; while((double)arr[i] <= ((double)n/(double)tmp)){ if((double)arr[i] >= ((double)m/(double)tmp)){ cnt++; } tmp = tmp * arr[i]; } } } System.out.println(cnt); } }
위 코드에서 유심하게 볼 부분은
long tmp = arr[i]; while((double)arr[i] <= ((double)n/(double)tmp)){ if((double)arr[i] >= ((double)m/(double)tmp)){ cnt++; } tmp = tmp * arr[i]; }
이 부분이다.
1. (double)arr[i] <= ((double)n/(double)tmp)
- 이는 다음 거듭제곱이 n을 넘지 않는지 확인
- tmp * arr[i] ≤ n 을 검사하는 것과 동일
- overflow를 방지하기 위해 나눗셈 형태로 변환
2. (double)arr[i] >= ((double)m/(double)tmp)
- 현재 거듭제곱이 m보다 크거나 같은지 확인
- tmp * arr[i] ≥ m 을 검사하는 것과 동일
- 마찬가지로 overflow 방지를 위해 나눗셈 사용
수학적인 개념이 적용되는 문제들은 아직 잘 모르겠다. 수학이 많이 약해서 생기는 현상이라 생각한다. 수학쪽을 좀 더 공부할 필요가 있을 것 같다.
'PS' 카테고리의 다른 글
| [Java] 백준 22858번 - 원상 복구 (small) (0) | 2024.09.12 |
|---|---|
| [Java] 백준 13023번 - ABCDE (2) | 2024.07.20 |
| 프로그래머스 - 주식가격 (스택/큐) (0) | 2023.05.10 |
| 프로그래머스 - 프로세스 (스택/큐) (0) | 2023.05.09 |
| 프로그래머스 - 다리를 지나는 트럭 (스택,큐) (0) | 2023.05.06 |
